Thinking in Three Dimensions
When we make representational art, it's important to have a grasp of volume and depth.
We want to depict objects with three dimensions, like they would be in the real world, but we have to do it in flat images that only have two dimensions.
We can standardize the three dimensions as up/down, left/right, and forward/backward. A combination of movements in these directions lets us go anywhere in 3D space.
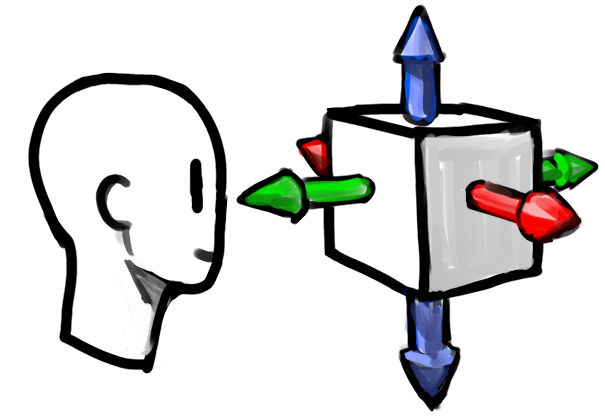
It's simple to apply the first two to a page or canvas, but third just doesn't exist in a flat image.
We might pretend the up/down of the paper is forward/backward, but we still lose a dimension.
One clever solution, an oblique projection, lets us keep the first two dimensions as they are, and then represent forward/backward at an angle.
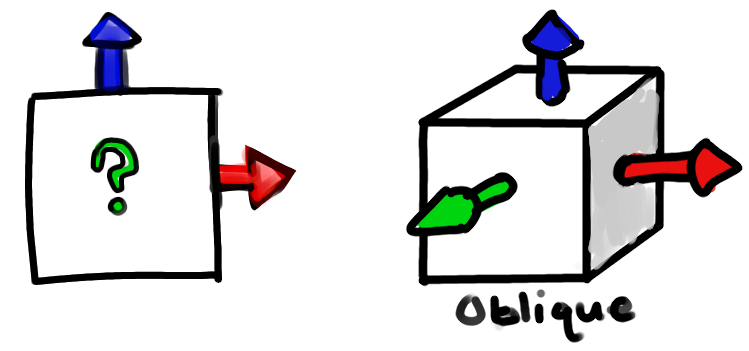
It isn't that realistic, but it's getting more believable.
Rather than depicting the objects themselves, we depict how they appear when looked at.
Depicting three dimensions as they appear is called perspective.
Linear Perspective
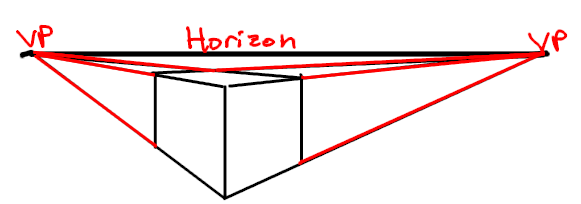
Perspective is commonly taught through something called linear perspective. It often comes in the form of 1-point or 2-point perspective, and sometimes 3-point. A problem I have with this is that it's often taught as a process without explaining what's happening. Establish the horizon line, the vanishing points, and then draw lines to the points. I won't go into detail on this, and I will be assuming you already know about it. If you don't already know linear perspective, I encourage you to go and learn it so the rest of this chapter might make more sense.
The core idea of perspective is pretty simple and easy to observe: Things look smaller when they get further away.
Look at an object. Walk away from it and look at it. It appears to get smaller, easy.

What if you kept walking straight, away from the object?
It would keep getting smaller and smaller. From very far away, it might get so small that you can't tell it's there. It vanishes. This is where vanishing points come from.
Horizons are the same thing. The visual change of the ground further away gets smaller and appears to stop eventually, forming a visual edge to the ground.
Get two objects near each other with a gap between. Walk away and look. The objects appear smaller again, but the gap should also appear smaller.
This would also vanish from far enough away.
Notice that the two objects get further away together in the same direction, and they converge to the same vanishing point. This is another important concept in perspective.
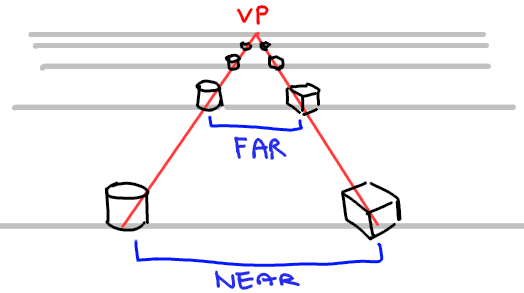
When different lines are drawn to the same vanishing point in linear perspective, it's because they are all edges that run in the same direction.
In 2-point perspective, the edges going to one vanishing point are going in one direction, and the edges going to the other point are going in a different direction.
But what might not be taught in a basic lesson is what if you wanted something in a direction other than what you've established a limited number of vanishing points for?
Well, it gets it's own vanishing point. You can have an infinite number of vanishing points in perspective because there's an infinite number of directions.
Stopping at 3 happens because 3 axes are enough to span the whole 3D space.
Eye Line vs Horizon Line
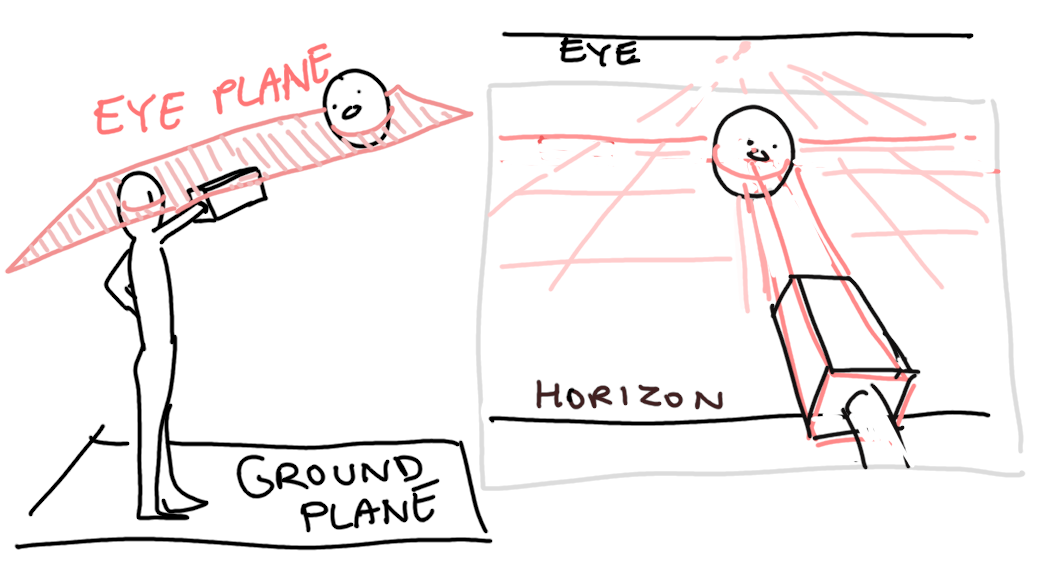
Let's quickly talk about eye line. It's like a horizon line, but comes from a plane level with the eye/camera instead of the ground plane. I like eye lines more than horizon lines, because there isn't always a horizon visible. Note that the eye line and horizon line are separate things. When eye is looking straight ahead, the plane level with the eye and the plane of the ground are parallel, then the lines will be in the same place. But if the eye looks up or down, the eye line will be above and below the horizon line respectively.
Curvilinear Perspective
I'm going to talk about curvilinear perspective now. It's a bit of an advanced topic, but it's really not that bad. Keep reading even if you're a beginner.
What you don't understand now might make sense later.
Linear perspective is a technique for mimicking an eye or camera, and works fine if the lens angle or field of view is narrow enough.
Curvilinear perspective is more accurate and works with very wide fields of view.
Look to your right, hold your hand up to your face, then move it directly away from your face.
It gets a little smaller as expected, and there would be a distant vanishing point off in that direction. Now look all the way to your left and do the same.
There's some distant vanishing point off in that direction as well. As long as your head was level, both of these points should be on the eye line, and
since they're directly across from each other, we can imagine a straight line between the points, passing through where your hands were.
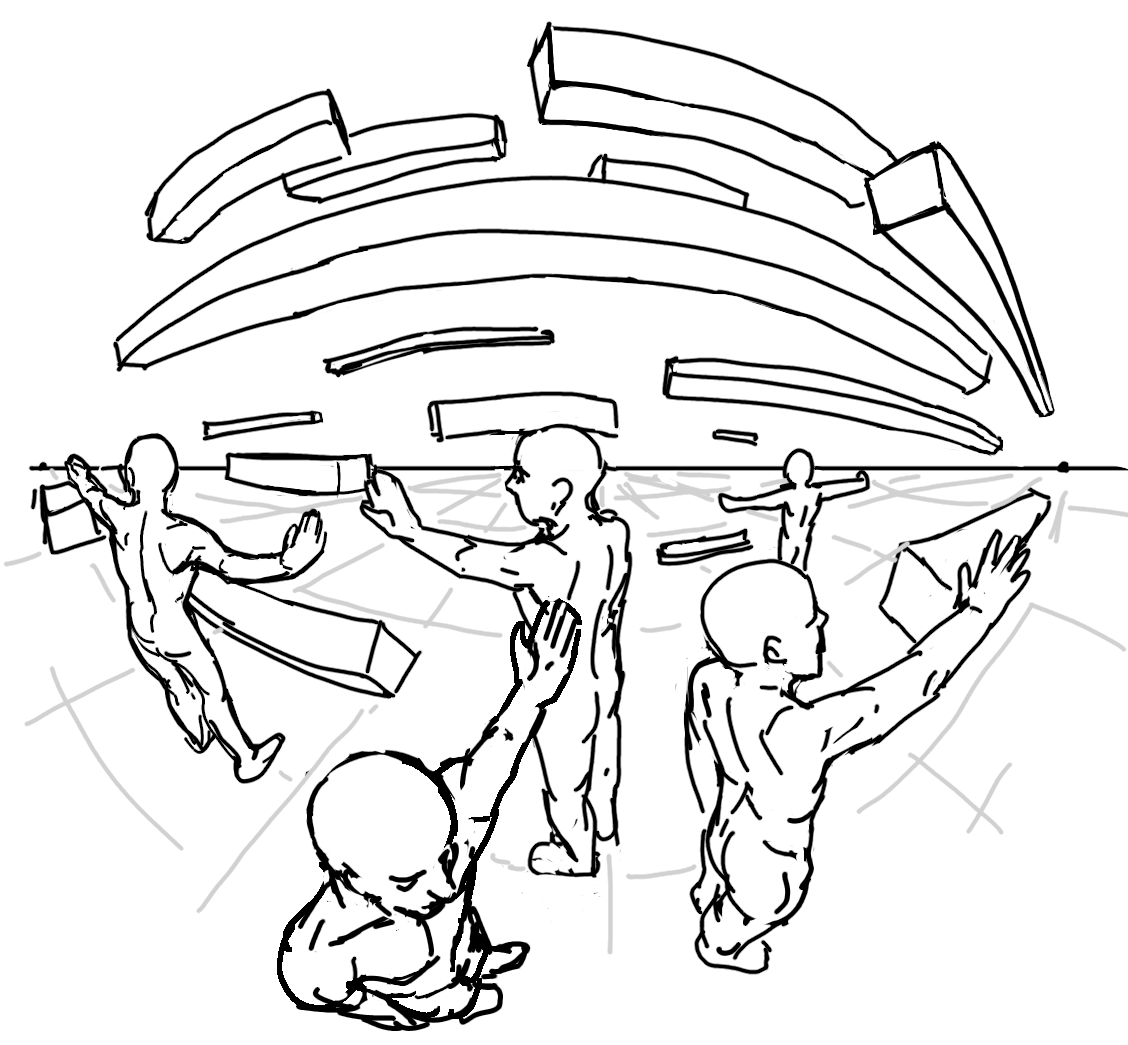
Imagine we have an extremely wide field of view so both the left and right vanishing points are in view, and that we're looking at a bunch of very long bars running parallel to the line.
The bars that are far away will appear near the eye line and seem to line up with it. But the bars that are closer need to somehow appear further away from the eye/horizon while their
ends still point towards and meet the vanishing points on the eye line. What happens is the straight lines closer to the viewer will appear to curve and bow out away from the
eye/horizon line. This produces the fisheye effect of a very wide lens angle.